高斯光束
高斯光束
石鑫华机器视觉网:在光学中,高斯光束(英语:Gaussian beam)是横向电场以及辐照度分布近似满足高斯函数的电磁波光束。许多激光都近似满足高斯光束的条件,在这种情况里,激光在光谐振腔里以TEM00波模传播。当它在镜片发生衍射,高斯光束会变换成另一种高斯光束,这时若干参数会发生变化。这解释了高斯光束是激光光学里一种方便、广泛应用的原因。
描述高斯光束的数学函数是亥姆霍兹方程的一个近轴近似解(属于小角近似的一种)。这个解具有高斯函数的形式,表示电磁场的复振幅。电磁波的传播包括电场和磁场两部分。研究其中任一个场,就可以描述波在传播时的性质。
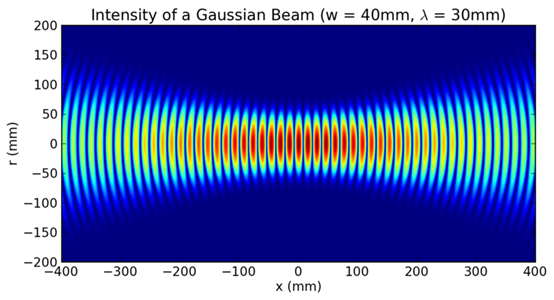
高斯光束的瞬时辐照度电脑绘图
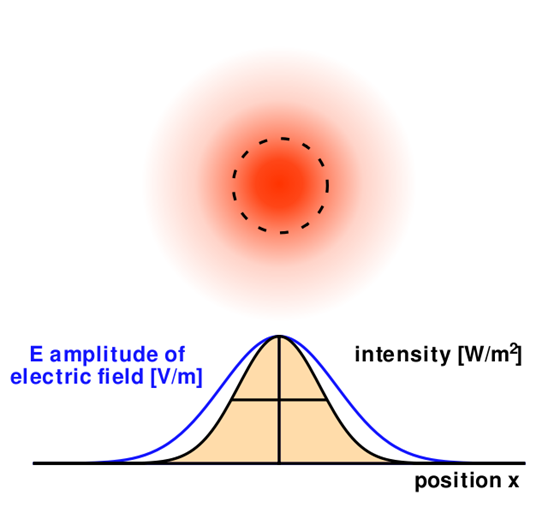
场强(蓝色)和辐照度(黑色)在坐标轴上的分布情况

纳米激光器产生的激光
数学形式
高斯光束作为电磁波,其电场的振幅为:
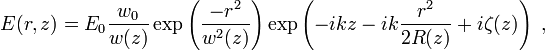
这里
 为场点距离光轴中心的径向距离
为场点距离光轴中心的径向距离
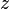 为光轴上光波最狭窄位置束腰的位置坐标
为光轴上光波最狭窄位置束腰的位置坐标
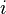 为虚数单位(即
为虚数单位(即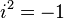 )
)
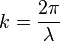 为波数(以弧度每米为单位)
为波数(以弧度每米为单位)
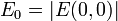 ,
,
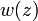 为电磁场振幅降到轴向的1/e、强度降到轴向的1/e2的点的半径
为电磁场振幅降到轴向的1/e、强度降到轴向的1/e2的点的半径
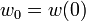 为激光的束腰宽度
为激光的束腰宽度
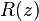 为光波波前的曲率半径
为光波波前的曲率半径
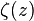 为轴对称光波的Gouy相位,对高斯光束的相位也有影响
为轴对称光波的Gouy相位,对高斯光束的相位也有影响
对应的辐照度时域平均值为
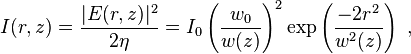
这里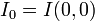 为光波束腰处的辐照度。常数
为光波束腰处的辐照度。常数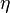 为光波传播介质的波阻抗在真空中,
为光波传播介质的波阻抗在真空中,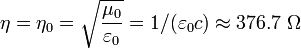 。
。
波束参数
高斯光束的许多性质由一系列波束参数决定,下面将分别予以介绍。
束宽
对于在自由空间传播的高斯光束,其腰斑位置的半径在光轴方向总大于一个最小值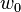 ,这个最小值被称为束腰。波长为
,这个最小值被称为束腰。波长为 的光波的腰斑位置在
的光波的腰斑位置在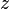 轴上的分布为
轴上的分布为
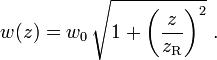
这里将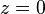 定义为束腰的位置。
定义为束腰的位置。
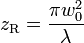
被称为瑞利距离。
瑞利距离和共焦参数
与束腰轴向距离等于瑞利距离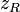 处的束宽为
处的束宽为
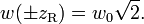
这两点之间的距离称作是共焦参数或光束的焦深。
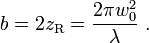
曲率半径
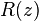 是光束波前的曲率半径,它是轴向距离的函数
是光束波前的曲率半径,它是轴向距离的函数
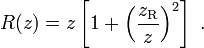
光束偏移
当 ,参数
,参数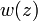 趋近于一条直线。这条直线与中央光轴的夹角被称为光束的“偏移”,它等于
趋近于一条直线。这条直线与中央光轴的夹角被称为光束的“偏移”,它等于
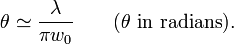
在原理束腰的位置,光束弯散的总角度为
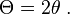
由于这一性质,聚焦于一个小点的高斯激光在远离这个点的传播过程中迅速散开。为了保持激光的准直,激光束必须具有较大的直径。束宽和光束偏移的这一关系是由于衍射的缘故。非高斯光束同样会表现这一效应,但是高斯光束是一种特殊情况,其束宽和偏移的乘积是可能达到的最小值。
由于高斯光束模型使用了近轴近似,当波前与光传播方向倾斜程度大于30度之后,这种模型将不再适用。通过上述偏移的表达式,这意味着高斯光束模型进队束腰大于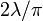 的光束适用。
的光束适用。
激光束的质量可以用束参数乘积来衡量。对于高斯光束,BBP的数值就是光束的偏移量与束腰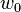 的乘积。实际光束的BPP通过计算光束的最小直径和远场偏移量的乘积来获得。在波长一定的情况下,实际光束的BPP数值与理想激光束的BPP数值的比值被称为“M2”。高斯光束的M2值为1,而所有的是激光束的M2值均大于1,并且质量越好的激光的M2值越接近1。
的乘积。实际光束的BPP通过计算光束的最小直径和远场偏移量的乘积来获得。在波长一定的情况下,实际光束的BPP数值与理想激光束的BPP数值的比值被称为“M2”。高斯光束的M2值为1,而所有的是激光束的M2值均大于1,并且质量越好的激光的M2值越接近1。
Gouy相位
光束的纵向相位延迟,或称Gouy相位为
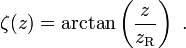
当光束通过焦点时,除了正常情况的相移,Gouy相移为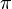 。
。
复数形式的光束参数
光束参数的复数为
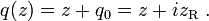
为了计算方便,常常使用它的倒数
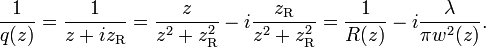
光束参数的复数形式在高斯光束传播的分析中有着重要地位,特别是分析它在光谐振腔中谐振过程时。
利用复数光束参数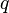 ,具有一个横向维度的高斯光束电磁场与下式成比例
,具有一个横向维度的高斯光束电磁场与下式成比例
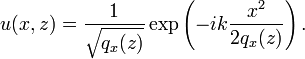
在二维的情况里,可以讲散光的光束表达为乘积的形式
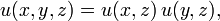
对于圆对称的普遍情况,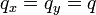 且
且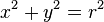 ,可以得出
,可以得出
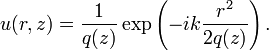
功率和辐照度
流经孔隙的功率
流经距离z轴半径为r的圆的功率为
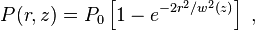
这里
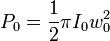 为电磁波传播的总能量
为电磁波传播的总能量
流经以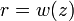 为半径的圆的能量占总能量的比值为
为半径的圆的能量占总能量的比值为
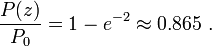
类似的,占光波总能量约95%的部分将流经半径为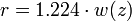 的圆形面积。
的圆形面积。
辐照度的峰值和平均值
在与束腰的轴向距离为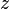 的位置,利用洛必达法则,可以计算该位置的辐射照度峰值
的位置,利用洛必达法则,可以计算该位置的辐射照度峰值
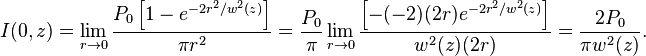
可以看出,辐照度峰值为平均值的两倍,后者等于总能量除以半径为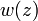 圆的面积。
圆的面积。
更多资源请登陆机器视觉论坛http://labviewvision.com。
上一篇:如何选择机器视觉LED光源
下一篇:雷射键盘
 售前咨询专员
售前咨询专员
