石鑫华视觉
在量子力学里，双缝实验（double-slit experiment）是一个测试量子物体像光或电子等等的波动性质与粒子性质的实验。双缝实验所需的基本仪器设置很简单。拿光的双缝实验来说，照射相干光波于一块内部刻出两条狭缝的不透明挡板。在挡板的后面，摆设了照相底片或某种侦测屏，用来纪录通过狭缝的光波的数据。从这些数据，可以了解光波的物理性质。参阅图 (1) ，光波的波动性质使得通过两条狭缝的光波互相干涉，造成了显示于侦测屏的明亮条纹和黑暗条纹，这就是双缝实验著名的干涉图案。可是，实验者又发觉，光波总是以一颗颗粒子的形式抵达侦测屏。
假若，光波是以粒子的形式从光源移动至侦测屏，那么，根据经典理论，抵达侦测屏某一位置的粒子数目应该等于在路途中，通过左狭缝的粒子数量与通过右狭缝的粒子数量的总和。换句话说，在侦测屏的任意位置，其明亮度应该等于遮掩左狭缝后的明亮度与遮掩右狭缝后的明亮度的总和。但是，实验者发觉，当两条狭缝都不被遮掩时，侦测屏某些位置会比较明亮，某些位置会比较黑暗。这图案只能用波动的建设性干涉和摧毁性干涉来解释，而不是粒子数量的简单加法。
双缝实验也可以用来测试像电子一类的粒子的物理行为，虽然使用的仪器不同，都会得到类似的结果，显示出波粒二象性。
理查德·费曼有一句他很喜欢的名言：仔细地思考双缝实验的意义，我们就能够一点一滴的了解整个量子力学。透过双缝实验，我们可以明了量子世界的真谛。
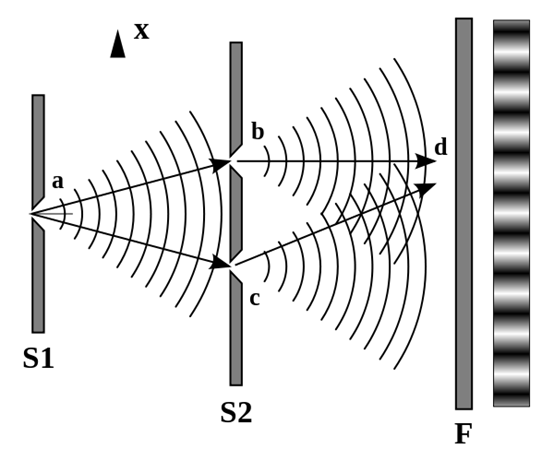
图 (1) ，双缝实验示意图，从光源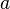 
传播出来的相干光波，照射在一块内部刻出两条狭缝 
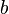和 
的不透明挡板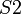 
。在挡板的后面，摆设了摄影胶卷或某种侦测屏 
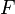，用来纪录到达 
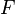的任何位置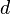 
的光波数据。最右边黑白相间的条纹，显示出光波在侦测屏 
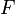的干涉图案。
图 (2) ，一块内部雕刻出两条狭缝的不透明挡板
自从哥本哈根诠释开始，物理界广泛地存在一种误解，那就是，为了决定光子从那一条狭缝经过而做的任何对于实验仪器的修改，也会连带地摧毁了干涉图案。这样，显示出粒子与波动的互补原理 (principle of complementarity)。于 1987 年完成的一个实验首先地发现了一个惊人的结果，那就是，哥本哈根诠释研讨的测量实验参数，只是一个连续值域的两个极端值。哥本哈根诠释忽略了其它在两个极端值之间的案例。假设，稍微改变参数值，则干涉图案也不会变得相差很大。在此之后完成的许多类似实验，也都证实了这实验的结果。请注意到，这些实验的实验者都能够在同一个实验里，观测到粒子现象和波动现象（例如，外村彰博士的电子双缝实验影音短片）。
本篇文章的许多论点可能会与这最新发现的结果有很大的落差。若有任何落差，最新结果应是比较及时的资讯。
图 (3) ，狭缝干涉实验，单缝 Vs. 双缝。两个实验都使用同样的双缝挡板（狭缝与狭缝距离为0,7mm)。在做单缝实验时，只有一条狭缝是打开的。单缝的干涉图案，一个主条纹和两旁较黯淡的条纹，也可以在双缝的干涉图案看到。但是，双侠缝的干涉图案显示出两倍的光强度，而且还出现了许多小干涉条纹。
如图(3) 所示，通常当只打开一条狭缝的时候，侦测屏会显示出单缝衍射的干涉图案，一条处于中央，比较明亮的条纹，旁边衬托著几条越来越黯淡的条纹。当打开两条狭缝的时候，侦测屏会显示出更明亮的干涉图案，每一条原本条纹都会进一步分裂成几个较细条纹。于 1803 年，托马斯·杨发表了一篇论文，《Experiments and Calculations Relative to Physical Optics》，详细阐述这些实验结果。根据光波是波动传播于媒体之间的假设，这些实验结果都可以用惠更斯-菲涅耳原理来解释清楚。但是，1887 年的光电效应发现，使得物理学家必须超越经典力学，更仔细地思考光的量子性质。
假设，我们稍微改变双缝实验，添加一个侦测仪器，专门侦测光子到底通过哪一条条纹，使我们能够知道光子通过的是那一条狭缝。那么，干涉图样会完全消失，我们不再能观测到干涉图样；替代显示出的是两个单缝图案的简单相加。这反直觉的而又容易制成的结果，给予物理学家无限的困惑。
假设，对于原本的双缝实验稍加变化。在任何时间，只发射一个光子。累积许多光子于摄影胶卷，我们会得到一个最令人迷惘的实验结果：干涉图案仍旧不改变。很清楚地，这意味着，虽然只有一个光子在移动，这光子的波包可以同时通过两条狭缝，自己与自己互相干涉！类似地，电子、原子、甚至分子，都可以表现出这奇异的量子行为。
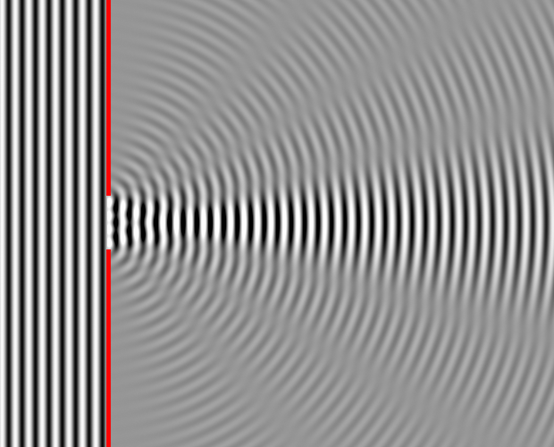
图 (4) ，单缝衍射图案
图 (5) ，双缝衍射图案
以波动观来解释光波的干涉，光波的波前同时地从两个狭缝凸涨出来，以同心圆图样传播出去。当波前传播至侦测屏的某一点时，两个光波的叠加，决定了光波会在那一点被观测到的强度。在侦测屏上观察到的明亮的条纹，是由光波的建设性干涉造成的，当一个波峰遇到另外一个波峰，建设性干涉会产生。黑暗的条纹是由光波的摧毁性干涉造成的，当一个波峰遇到另外一个波谷，摧毁性干涉会产生。图 (7) 展示光波的传播与干涉。
以粒子观来解释，光子的量子行为可以用概率波来描述，当概率波的波前传播至侦测屏的某一点时，两个概率波的叠加，决定了光子会移动到那一点的概率。更详细的说，两个概率波的概率幅相加后，取绝对值平方，就是这概率。经过累积许多光子后，我们可以在侦测屏观测到一系列的条纹。图 (7) 展示概率波的传播与干涉。
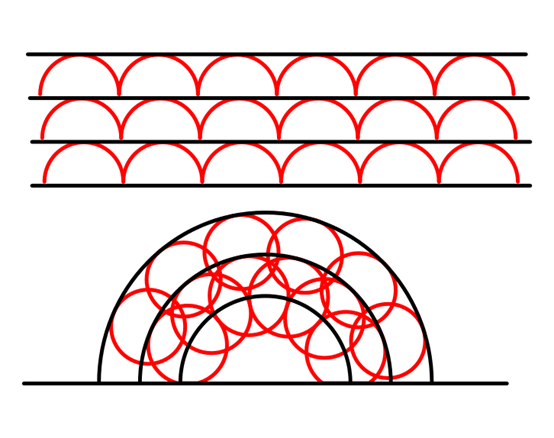
图 (8) 展示怎样用惠更斯的方法来延伸一个平行波前，怎样来延伸一个圆形波前。一组同尺寸的，圆心包含于一个波前的圆圈。它们的切线，经过联结与平滑后，形成一条连续的曲线，这就是预测的波前位置。
克里斯蒂安·惠更斯发现了光波传播的基本原理，怎样预测光波的传播于介质。光源发放出一连串的光波，就好似浮在水面上的浮标，被重复的拉起来，放下去，造成了水波的传播。他想出一种预测波前位置的方法。参阅图 (8) ，制造一组同尺寸的，圆心包含于一个波前的圆圈。它们的切线，经过联结与平滑后，形成一条连续的曲线，这就是预测的波前位置。依照这方法，可以展示出一个平面波前，或一个圆形波前，延伸的状况。根据惠更斯的理论，奥古斯丁·菲涅耳证明了光的波动性貭和光在纯介质内以直线传播的射线行为，并没有任何矛盾。他又照着惠更斯的点子，对于衍射与干涉现象，给予了一个合理、完整的解释。详尽细节，请参阅惠更斯-菲涅耳原理。
随着量子力学的发展，物理学家对于光波的物理性质有更多的了解。在一段短暂的时间内，传播至某一表面的一束光波意味着许多光子的到达。每一个光子都有它自己的波前。为了要了解在双缝实验里，真正发生了什么状况，物理学家必须知道，假设光子是一个一个的发射出来的，那么，会观测到什么状况？1909 年，为了解答这问题，杰弗里·泰勒爵士做了一个很精致的双缝实验。这实验将入射的光波强度大大减低，在每单位时间内，平均只有一粒光子被发射出来。每一个光子的波前通过两条狭缝后，这光子会显示于侦测屏的某个位置的概率，可以由通过两条狭缝后的两个概率波，在那位置的概率幅计算出来。两个概率幅的相加，取绝对值平方，就是概率。累积许多光子抵达侦测屏的位置数据，泰勒爵士发现，显示于侦测屏的干涉图案与原本的双缝实验图案相同。
英国物理学者托马斯·杨
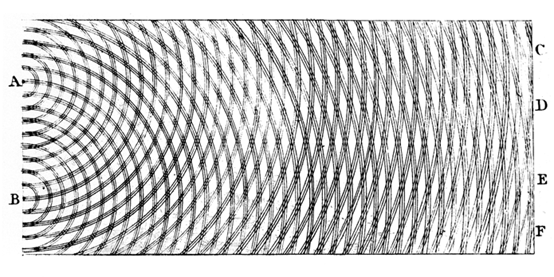
图 (9) ，根据实验观察的水波图样，托马斯·杨亲手绘制的双缝干涉现象
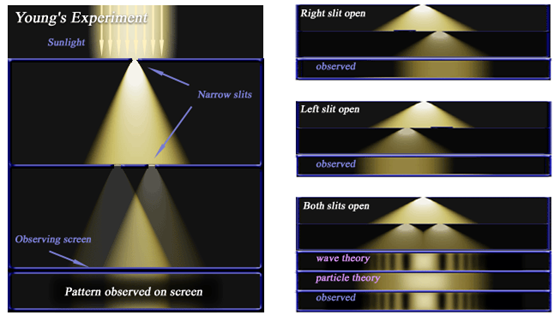
图 (10) ，托马斯·杨设计与研究成功的双缝实验。用经典的粒子观解释，不会产生干涉现象；只有用波动观，才会产生干涉现象
双缝实验最先是由英国科学家托马斯·杨设计与研究成功的。1801年，为了了解光到底是粒子还是波动，他设计了这精巧又美丽的实验。如图 (9) 、(10) ，从这实验观测到的干涉图案给予光的粒子观一个致命的打击。因为，经典的粒子理论无法满意地解释这实验的干涉图案。大多数的科学家从此接受了光的波动观。一直到 20 世纪初期，才又有出现支持粒子观的实验证据。由于它可以很清楚简易地，探讨量子力学的中心迷云，双缝实验与它的各种变异版，成为了许多理论物理家宠爱的思想实验。
1972年，理查德·西利托与 C ·威克斯（C.Wykes）将双缝实验修改，使得在任何时间，只有一条狭缝是开启的，另外一条狭缝是关闭的。还有，光子的密度超小于 1 。这样，在任何时间，光子只能经过两条狭缝中的一条狭缝。虽然如此，假若侦测的光子可能通过任意一条狭缝，他们仍旧观测到光子的干涉图案。
1961年，蒂宾根大学的克劳斯·约恩松（Claus Jönsson）创先地用电子来做双缝实验，他发现电子也会有干涉现象。1974年，皮尔·梅利（Pier Merli) ，在米兰大学的物理实验室里，成功的将电子一粒一粒的发射出来。在侦测屏上，他也确实地观测到干涉现象。2002年9月，约恩松的双缝实验，被《Physics World》杂志的读者，选为最美丽的物理实验。
参阅图 (1) ，在任何时刻，用一个波前来代表那时刻所有从光源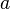 
传播出来的光波。通过两条狭缝后，波前衍散出来，在侦测屏行成的干涉图样中，任何两个部分的距离 
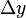，会随着挡墙与侦测屏的距离 
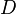而变。假若 
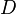增加，则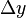 
也增加。减小两条狭缝 
，
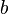之间的距离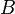 
，会增加条纹之间的距离。增加光波的波长 
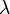，也会增加条纹之间的距离。可是，狭缝的缝宽的尺寸必须适当，能够允许光波通过。否则，单缝干涉效应会变得很显著，因而盖压过双缝实验效应。反过来说，假若，狭缝太宽（例如，一座墙上的两扇普通的窗子），则光波会直接照射过去，就观察不到干涉现象了。
在侦测屏上观察到的明亮的条纹，是由光波的建设性干涉造成的，当一个波峰遇到另外一个波峰，建设性干涉会产生。黑暗的条纹是由光波的摧毁性干涉造成的，当一个波峰遇到另外一个波谷，摧毁性干涉会产生。用方程表达，当以下关系成立时，会发生建设性干涉：
；
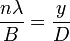其中，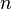
是最大强度值（波峰遇到波峰，最大建设性干涉的光波强度）的次序数（位于中央的最大强度值的次序数是 
），
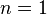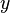是条纹与中央之间的距离（称为条纹距离）。
这方程只是一个近似。方程的成立依赖某些先决条件的成立。应用这方程于实验仪器，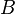
和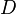 
是实验参数，
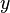可以由实验测量得知，有了这几个数值，我们就可以计算应该使用哪种波长的光波。
图 (11) ，经过一段时间，电子的累积显示出干涉图案
在 1920 年代，从许多实验结果，像光电效应，物理学家发觉光波是以离散的，粒子的形式，称为光子，与物质相互作用。
假设，有一种光源能够一个个地发射光子，而且，侦测屏有足够的敏感度来侦测单独一个光子。则杨式双缝实验，在理论上，可以用光子一个个的测试，得到的结果会与原本实验的结果相同。经过一段时间的累积光子，侦测屏会展示出一系列明亮或黑暗的条纹的干涉图样。这结果看来好像又确定，又否定波动观。假若，光的行为不是波动行为，则侦测屏不会展示出干涉图案。假若，光的波动观成立，则光不会以量子的形式抵达侦测屏。
让我们特别注意一个卓越的实验。在这实验里，有一个侦测器，称为“狭缝侦测器”，能够侦测到光子的行踪，光子会经过两条狭缝中的哪一条狭缝。可是，当我们将狭缝侦测器打开后，我们所熟悉的干涉图案，立刻就会消失不见，转而改变成另外一种图案。侦测这个动作，涉及了光子与狭缝侦测器之间的相互作用。这改变了光子的量子态。假设，两个同频率的光子，在同时间被发射出来，则这两个光子是相干的。将狭缝侦测器关掉，则两个相干光子，都会不被干擾地经过狭缝，相干地抵达侦测屏。可是，假设，我们将狭缝侦测器打开，而两个相干光子之中的一个光子，被狭缝侦测器侦侧到，则由于光子与狭缝侦测器之间的相互作用，两个光子不再互相干涉。所以，侦测屏的干涉图案会消失不见。
在早期的量子力学里，许多先驱学者的共识，哥本哈根诠释，明确地阐明，我们不应该超越数学公式和精确实验给予的结果的范围，大胆假设任何其它理论，使我们因而得到任何涉及量子尺寸的知识。概率波是一个数学构造，能够给予物理学家预测某些实验结果的能力。它的数学形式类比物理波动的描述。概率波概率幅的絶对值平方给予某些可观测物理现象发生的概率。应用概率波的概念于双缝实验，物理学家可以计算出粒子抵达侦测屏的某位置的概率。
除了光子发射的时间与抵达侦测屏的时间以外，在任何其它时间，我们不能够确定光子的位置。为了要确定光子在某个其它时间的位置，我们必须侦测到它。可是，一当我们侦测到光子在某个其它时间的位置，我们也改变了光子的量子态，干涉图案也因此受到影响。所以，在发射的时间与抵达侦测屏的时间之间，我们无法知道光子的位置。我们只知道，在发射的时候与抵达侦测屏的时候，光子是存在的。在其它时间，光子完全地跟我们的宇宙失去了连络。在双缝实验里，到底发生了什么状况，我们无从得知。
一个光子，从被太阳发射出来的时间，到抵达我们的视网膜，引起视网膜的反应的时间，在这两个时间之间，我们完全不知道，发生了什么关于光子的事。或许这论点并不会很令人惊讶。可是，从双缝实验，物理学家发现一个很值得注意的结果，假若，我们试着确定光子在发射点与侦测屏之间的位置，我们也会改变双缝实验的结果。假若，我们用狭缝侦测器，来侦测光子会经过两条狭缝中的那一条狭缝，则原本的干涉图案会消失不见。假若，在光子抵达侦测屏之前，我们又将这狭缝侦测器所测得的资料摧毁，那么，干涉图案又会重现于侦测屏（参阅 量子擦除实验 (quantum eraser experiment) ）。双缝实验的程序与结果奇异地连结在一起。
路径积分表述是理查·费曼提出的一个理论（费曼强调这个表述只是一个数学描述，而并不是描述某些我们无法观察到的真实程序的尝试。）。路径积分表述阐明，假设一个光子要从发射点 a 移动至侦测屏的位置点 d ，它会试着选择经过所有的可能路径，包括选择同时经过两条狭缝的路径。可是，假若，我们用狭缝侦测器，来侦测光子会经过两条狭缝中的那一条狭缝，实验的状况立刻改变了。狭缝侦测器的位置变为点 d 。新的路径是从狭缝侦测器 d 到侦测屏 d' 。这样，在狭缝侦测器 d 与侦测屏 d' 之间，只有空旷的空间，并没有两条狭缝。所以，不会有干涉图案。
不论是电子、质子，或是任何其它量子尺寸的粒子，在双缝实验里，粒子抵达侦测屏的位置的概率分布，是具有高度决定性的。我们可以用量子力学来精确地计算与预测，粒子抵达侦测屏的某位置的概率。可是，我们无法预侧，在什么时刻，在侦测屏的什么位置，会有一个粒子抵达。这么一个无可争议的结果，是经过多次重复地实验而得到的。这结果给予了科学家极大的困惑。因为粒子抵达顺序的无法预测，意味着没有任何原由，而发生的事件，这是科学家非常不愿意接受的事实。他们试图制造更多的变量来解决这困难。
当电子一堆一堆地对着侦测屏发射，我们可以很容易地解释所产生的干涉图案。我们只要认定这些电子互相地干涉。可是，随着科技地进步，现在已经发展出来，能够可靠地发射单独电子的科学器材。应用这单独电子发射器于双缝实验，得到的干涉图案，使我们觉得好像电子有独自干涉自己的可能，又觉得好像单独的电子可以同时通过两条狭缝。对于大多数的科学家，这似乎建议，量子粒子能够同时出现于两个以上的地方。可是这建议与显然正确的道理，“任何事件不能同时地发生在两个地方”，有很大的落差（参阅无矛盾律）。对于这问题，最简单的方法，就是接受物质波的概念。另外一种比较不容易被接受的概念，主张量子物质的存在与行为，是无法用经典方法来诠释的。这种概念，与我们日常体验的物理事实有很大的出入，会造成更多的困惑。
单独电子累积的双缝实验干涉图案，与一堆电子的双缝实验干涉图案，两个干涉图案是相同的。所以，我们可以维持一个有秩序的，一致的宇宙观。虽然，对于任何量子尺寸的粒子，我们必须以物质波来看待。
近几年来的科学研究，更进一步地发现了，干涉现象并不只限制于像质子、中子、电子、等等，这些基本粒子。双缝实验使用大分子构造，像富勒烯 (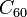 
) ，也能够产生类似的干涉图案。