光速
光速
光速,即光波传播的速度。真空中的光速是一个重要的物理常数,符号为c(来自拉丁语中的 celeritas,意为迅捷),c不仅仅是可见光的传播速度,也是所有电磁波在真空中的传播速度。
真空中的光速等于299,792,458米/秒(1,079,252,848.8千米/小时)。这个速度并不是一个测量值,而是一个定义。它的计算值为(299792500±100)米/秒。国际单位制的基本单位米于1983年10月21日起被定义为光在1/299,792,458秒内传播的距离。使用英制单位,光速约为186,282.397英里/秒,或者670,616,629.384英里/小时,约为1英尺/纳秒。
在任何透明或者半透明的介质(比如玻璃和水)中,光速会降低;c比光在某种介质中的速度就是这种介质的折射率。引力的改变能够弯曲光所传播的空间,使光像通过凸透镜一样发生弯曲,看上去绕过了质量较大的天体。光弯曲的现象叫做引力透镜效应,根据变化了的光线在光谱外波段呈现的不规则程度,可以推算发光星系的年龄和距离。
根据爱因斯坦的相对论,没有任何物体或信息运动的速度可以超过真空中的光速(c)。
奥勒·罗默在1676年凭借研究木星的卫星木卫一的视运动第一次表明了光是以有限的速度(而不是立刻地)在传播。在1865年,詹姆斯·克拉克·麦克斯韦提出光是一种电磁波,因此在他的电磁理论中应该以速度“c”来传播。在1905年,阿尔伯特·爱因斯坦假定光速就任何惯性系而言,是独立于光源的运动的。他还通过推导狭义相对论探索了这个假设的后果。结果显示参数“c”在光和电磁背景之外有相关性。经过几个世纪的越来越精确的测量,光的速度在1975年被得知为299,792,458 m/s(有十亿分之四的测量误差)。1983年,在国际单位制中米被重新定义为光在真空中传播1⁄299,792,458秒的距离。因此根据米的定义,“c”以米每秒所表示的数值就被固定下来。
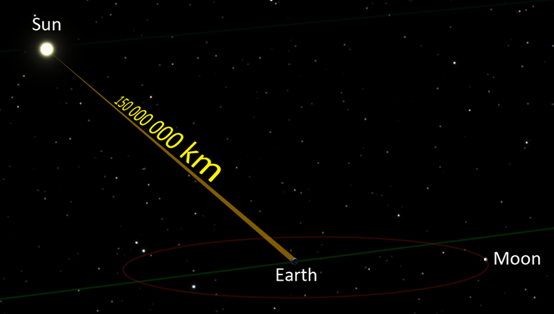
阳光要花费大约8分19秒才能到达地球(基于平均距离)
光速的物理
接近光速情况下,笛卡尔坐标系不再适用。同样测量光线离开自己的速度,一个快速追光的人与一个静止的人会测得相同的速度(光速)。这与日常生活中对速度的概念有异。两车以50km/h的速度迎面飞驰,司机会感觉对方的车以50 + 50 = 100km/h行驶,即与自己静止而对方以100km/h迎面驶来的情况无异。但当速度接近光速时,简单加法计算速度不再奏效。当两飞船以90%光速的速度(对第三者来说)迎面飞行时,船上的人不会感觉对方的飞船以90% + 90% = 180%光速速度迎面飞来,而只是以稍低于99.5%的光速速度行驶。结果可从爱因斯坦计算速度的算式得出:
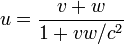
其中v和w是对第三者来说飞船的速度,u是感受的速度,c是光速。
介质中的光速
折射率大于1时,有两种情况,相速度低于 c,群速度高于 c; 折射率小于1时,相速度高于 c,群速度低于 c; 下图为折射率大于1的情形。
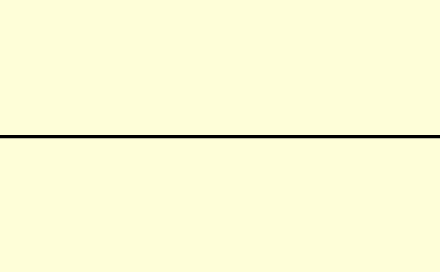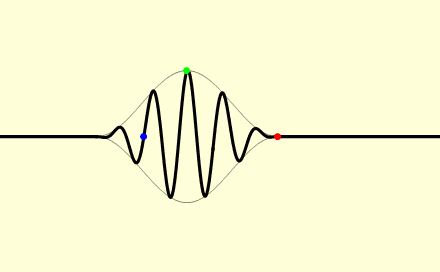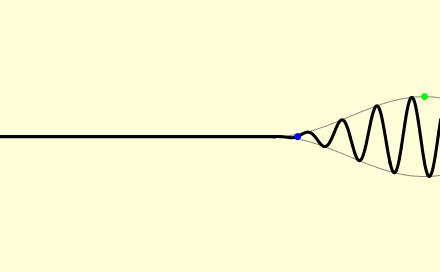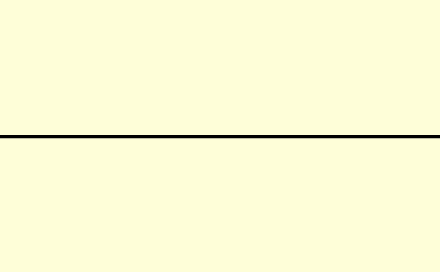
图中蓝点以相速度移动,绿点以群速度移动,而红点以波前速度移动
光速的测量
最早光速的准确数值是通过观测木星对其卫星的掩食测量的。还有旋转齿轮法、转镜法、克尔盒法、变频闪光法等光速测量方法。
根据现代物理学,所有电磁波,包括可见光,在真空中的速度是常数,即是光速。强相互作用、电磁作用、弱相互作用传播的速度都是光速,根据广义相对论,万有引力传播的速度也是光速,且已于2003年得以证实。根据电磁学的定律,发放电磁波的物件的速度不会影响电磁波的速度。结合相对性原则,观察者的参考坐标和发放光波的物件的速度不会影响被测量的光速,但会影响波长而产生红移、蓝移。这是狭义相对论的基础。相对论探讨的是光速而不是光,就算光稍微减慢,也不会影响狭义相对论。

光线从地球到月球仅需约 1.255 秒、
早期
一些早期的物理学家,包括弗兰西斯·培根、约翰内斯·开普勒和勒内·笛卡儿在内,都普遍认为光速是无限的。艾萨克·毕克曼最早在1629年提出一项试验,一人将闪光灯反映一面镜子,约一英里,以测量光速。伽利略认为光速是有限的,1638年他请二个人提灯笼各爬上相距仅约一公里的山上,第一个人掀开灯笼,并开始计时,对面山上的人看见亮光后掀开灯笼,第一个人看见亮光后,停止计时。这是史上著名的测量光速的掩灯方案,但由于光速实在太快,所以实验没有成功。
天文观测法
1676年,奥勒·罗默使用望远镜研究木星的卫星艾欧的运动,第一次定量的估计出光速。艾欧的公转轨道可以用来计算时间,因为它会规律的进入木星的阴影中一段时间(图中的C至D)。罗默观测到当地球在最接近木星时(H点),艾欧的公转周期是42.5小时,当地球远离木星时(从L至K),艾欧从阴影中出现的时间会比预测的越来越晚,很明显的是因为木星与地球的距离增加,使得"信号"要花更多的时间传递。光要通过行星之间增加的距离,使得计时的信号在第一次和下一次之间因而延长了额外的时间。当地球向木星接近时(从F到G),情形则正好相反。罗默观测到艾欧在接近的40个轨道周期中周期比远离的40个轨道周期缩短22分钟。罗默以这些观测为基础,认为在80个轨道周期中光线要多花费22分钟行走艾欧与地球之间增加的距离。这意味着从L至K和F至G,地球经历80个艾欧轨道周期(42.5小时)的时间,光线只要花22分钟。这对应于一个地球在轨道上绕着太阳运动和光速之间的一个比例:
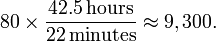
意味着光速是地球的轨道速度的9,300倍,与现在的数值10,100倍比较,相差无几。
天文单位在当时的估计数值是大约1亿4千万公里。克里斯蒂安·惠更斯结合了天文单位和罗默的时间估计光速每分钟的速度是地球直径的1,000倍,他似乎误解罗默22分钟的意思,以为是横越地球轨道所花费的时间。这相当于每秒220,000公里(136,000英里),比现在采用的数值低26%,但仍比当时使用其他已知的物理方法测得的数值为佳。
艾萨克·牛顿也接受光速是有限的观念,在他1704年出版的书光学中,提出光每秒钟可以横越地球16.6次(相当于210,000公里/秒,比正确值低了30%)。这似乎是他自己的推断(不能确知他是否有引用或参考罗默的数据)。罗默随后依据同样的原理观察木星表面上的斑点在自转周期上的变化,也观察其他三颗伽利略卫星的相同现象。但是因为这种观测是很困难的,因而日后被其他的方法所取代。
即使如此,靠着这些观测,光速是有限的仍不能被大众满意的接受(包括著名科学家吉恩·多米尼克·卡西尼),直到在詹姆斯·布雷德里(1728)的观测之后,光速是无限的想法才被扬弃。布雷德里推论若光速是有限的,因为地球的轨道速度会使抵达地球的星光有一个微小角度的偏折,这就是所谓的光行差,它的大小只有1/200度。布雷德里计算的光速为298,000公里/秒(185,000英里/秒),与现在的数值只有不到1%的差异。光行差的效应在19世纪已经被充分的研究,最著名的学者是瓦西里·雅可夫列维奇·斯特鲁维和de:Magnus Nyrén。
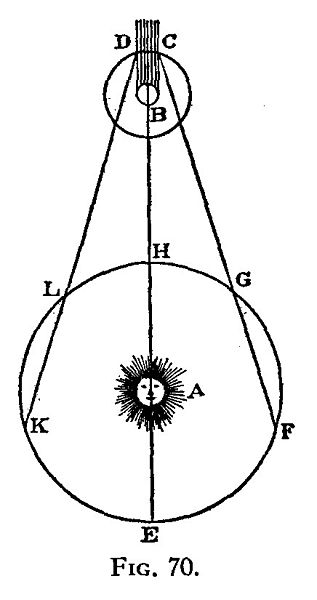
罗默从地球观测木卫一的掩蔽来测量光速
机械测量
1849年,阿曼德·斐索用旋转齿轮法求得 c = 3.153×108 m/s。他是第一位用实验方法,测定地面光速的实验者。实验方法大致如下:
光从半镀银面反射后,经高速旋转的齿轮投向反射镜,再沿原路返回。如果齿轮转过一齿所需的时间,正好与光往返的时间相等,就可透过半镀银面观测到光,从而根据齿轮的转速计算出光速。
1862年,莱昂·傅科用旋转镜法测空气中的光速,原理和斐索的旋转齿轮法大同小异,他的结果是 c = 2.98 × 108 m/s。
第三位在地面上测到光速的是考尔纽(M.A.Cornu)。1874年他改进了斐索的旋转齿轮法,得 c = 2.9999 × 108 m/s。
阿尔伯特·迈克耳孙改良傅科的旋转镜法,多次测量光速。1879年,得 c = (2.99910±0.00050) ×108 m/s;1882年得 c = (2.99853±0.00060) × 108 m/s。
后来,他综合旋转镜法和旋转齿轮法的特点,发展旋转棱镜法,1924~1927年间,得 c = (2.99796±0.00004) × 108 m/s。
迈克耳孙在推算真空中的光速时,应该用空气的群速折射率,可是他用的却是空气的相速折射率。这一错误在1929年被伯奇发觉,经改正后,1926年的结果应为 c = (2.99798±0.00004) × 108 m/s = 299798±4 km/s。
后来,由于电子学的发展,用克尔盒、谐振腔、光电测距仪等方法,光速的测定,比直接用光学方法又提高一个数量级。
60年代激光器发明,运用稳频激光器,可以大大降低光速测量的不确定度。
1973年达0.004 ppm,终于在1983年第十七届国际计量大会上做出决定,将真空中的光速定为精确值。
光速测量年表
年代 | 主持人 | 方式 | 光速(千米/秒) | 不确定度(千米/秒) |
1849 | 阿曼德·斐索 | 旋转齿轮法 | 315 300 | |
1862 | 莱昂·傅科 | 旋转镜法 | 298 000 | 500 |
1907 | Rosa、Dorsey | ESU/EMU¥ | 299 784 | 15 |
1928 | Karolus 等 | 克尔盒 | 299 786 | 15 |
1947 | Essen 等 | 谐振腔 | 299 792 | 4 |
1949 | Aslakson | 雷达 | 299 792.4 | 2.4 |
1951 | Bergstand | 光电测距仪 | 299 793.1 | 0.26 |
1954 | Froome | 微波干涉仪 | 299 792.75 | 0.3 |
1964 | Rank 等 | 带光谱 | 299 792.8 | 0.4 |
1972 | Bay 等 | 稳频氦氖激光器 | 299 792.462 | 0.018 |
1973 | 平差 | 299 792.4580 | 0.0012 | |
1974 | Blaney | 稳频CO2激光器 | 299 792.4590 | 0.0006 |
1976 | Woods 等 | 299 792.4588 | 0.0002 | |
1980 | Baird 等 | 稳频氦氖激光器 | 299 792.4581 | 0.0019 |
1983 | 国际协议 | (规定) | 299 792.458 | (精确值) |
¥ESU即Electrostatic units的缩写;EMU为Electromagnetic units的缩写。
 售前咨询专员
售前咨询专员
